Рациональное поведение. Часть 1. Ошибки при принятии решений. Теорема Байеса
Видео и статья на тему «Основы рационального поведения»
На данном уроке мы рассмотрим тему, которая не входит в школьную программу, но тем не менее является очень полезной в повседневной жизни: какие ошибки мы совершаем при принятии решений и почему анализы на редкие болезни нужно делать как минимум дважды (и причём тут теорема Байеса).
Кто украл деньги? (00:00)
Представим ситуацию, когда из сейфа пропали деньги (Рис.1). Если провести опрос на тему «Кто украл деньги – вор или вор-рецидивист?», большинство ответит: это был вор-рецидивист. На самом деле если больше ничего не известно о данной ситуации, вероятность того, что это был просто вор, выше.

Рис. 1. Кража денег из сейфа
С другой стороны, понятно, почему при опросе большинство выбрало вора-рецидивиста. Это связано с тем, что поиски разумно начинать именно среди воров-рецидивистов.
В качестве аналогичного примера можно привести опрос, который проводил Дэниел Канеман. Суть опроса заключалась в выборе более вероятного из двух событий:
Большинство людей проголосовало за второй вариант. Но ведь это более узкое событие, а первое событие (в Америке произошло наводнение) более общее и включает в себя все возможные исходы (все ситуации, в результате которых произошло наводнение). Возможно, если бы людям дали немного больше времени подумать, они выбрали бы первый вариант.
В качестве аналогичного примера можно привести опрос, который проводил Дэниел Канеман. Суть опроса заключалась в выборе более вероятного из двух событий:
- в Америке произошло наводнение,
- из-за цунами в штате Калифорния в Америке произошло наводнение
Большинство людей проголосовало за второй вариант. Но ведь это более узкое событие, а первое событие (в Америке произошло наводнение) более общее и включает в себя все возможные исходы (все ситуации, в результате которых произошло наводнение). Возможно, если бы людям дали немного больше времени подумать, они выбрали бы первый вариант.
В результате этого опыта был сделан важный вывод: люди охотнее верят в события, для которых сразу указана причина. Эта причина для большинства людей играет роль подсказки и несет в себе эмоциональную составляющую.
Этот тип мышления часто используют мошенники для манипуляции. Поэтому очень важно знать причины возникновения подобных ситуаций.
Среди нашей рабочей группы также проводились подобные опросы. Оказалось, что те, у кого есть техническое (математическое) образование, хоть иногда и сомневались, но в конечном итоге правильно отвечали, а люди без технического образования отвечали зачастую неправильно, эмоционально реагировали на опрос и пытались доказать свою правоту.
Среди нашей рабочей группы также проводились подобные опросы. Оказалось, что те, у кого есть техническое (математическое) образование, хоть иногда и сомневались, но в конечном итоге правильно отвечали, а люди без технического образования отвечали зачастую неправильно, эмоционально реагировали на опрос и пытались доказать свою правоту.
Определение более вероятного события (02:32)
Рассмотрим, как определить более вероятное событие на примере с наводнением. Изобразим схематически в виде круга все возможные причины наводнения (цунами, землетрясение и т.д.). На этом же круге изобразим конкретную причину наводнения (цунами), то есть одну из всех возможных причин (Рис. 2).

Рис. 2. Схематическое изображение вероятности наводнения
Если заменить вероятность бросанием дротиков вслепую, то в большой круг мы попадём с большей вероятностью, чем в маленький.
Как мы уже говорили, в подобных ситуациях люди могут принимать нерациональное решение. Этим пользуются, например, страховые компании. В результате чего люди охотнее страхуются от частных случаев, которые постоянно на слуху, хотя более общая страховка может быть дешевле или равной по стоимости. Люди выбирают более узкое направление страховки вместо общего из-за психологического фактора.
Можно застраховаться только от терроризма или за ту же цену застраховаться от катастроф, в которые включен терроризм. Если человека больше волнует терроризм, то он с большей вероятностью застрахуется только от него, но рациональнее страховаться от всех катастроф (в том числе от терроризма).
Аналогично можно страховать машину от повреждений, вызванных падением какого-либо предмета или от падения льдины на машину. В северных районах кажется, что случай падения льдины более вероятен, поэтому зачастую там выбирают второй вариант страховки. Хотя страховка от падения какого-либо предмета включает в себя падение льдины. В этом и заключается психологический фактор.
Бывает, что подобные ситуации нелегко распознать в силу того, что формулировка завуалирована или по какой-то другой причине. Очень часто в рекламе используется подобный трюк, когда известные люди рекламируют какой-нибудь товар или услугу. Это рассчитано на то, что люди доверяют выбору знаменитости и следуют за ним, хотя на самом деле подавляющее большинство других знаменитых людей выбирают какой-то другой продукт.
Как мы уже говорили, в подобных ситуациях люди могут принимать нерациональное решение. Этим пользуются, например, страховые компании. В результате чего люди охотнее страхуются от частных случаев, которые постоянно на слуху, хотя более общая страховка может быть дешевле или равной по стоимости. Люди выбирают более узкое направление страховки вместо общего из-за психологического фактора.
Можно застраховаться только от терроризма или за ту же цену застраховаться от катастроф, в которые включен терроризм. Если человека больше волнует терроризм, то он с большей вероятностью застрахуется только от него, но рациональнее страховаться от всех катастроф (в том числе от терроризма).
Аналогично можно страховать машину от повреждений, вызванных падением какого-либо предмета или от падения льдины на машину. В северных районах кажется, что случай падения льдины более вероятен, поэтому зачастую там выбирают второй вариант страховки. Хотя страховка от падения какого-либо предмета включает в себя падение льдины. В этом и заключается психологический фактор.
Бывает, что подобные ситуации нелегко распознать в силу того, что формулировка завуалирована или по какой-то другой причине. Очень часто в рекламе используется подобный трюк, когда известные люди рекламируют какой-нибудь товар или услугу. Это рассчитано на то, что люди доверяют выбору знаменитости и следуют за ним, хотя на самом деле подавляющее большинство других знаменитых людей выбирают какой-то другой продукт.
Мы часто проверяем гипотезу в одну сторону, не проверяя в обратную. В этом заключается ошибка выбора.
Рассмотрим фразу «200 миллионов китайцев не могут ошибаться». Но если все эти китайцы курят, то это не значит, что они правильно поступают и все остальные должны начать курить.
Приведем пример из древности. Когда Цицерону (древнеримскому политическому деятелю и философу) показали фреску с изображением, где люди молятся, чтобы спастись от шторма, и фреску с людьми, которые спаслись, потому что молились, он попросил изображение с людьми, которые молились и не спаслись. То есть, возвращаясь к вероятности, мы иногда видим некую часть поля событий, но из-за своих эмоциональных или психологических особенностей не видим его в целом.
С помощью этого эффекта пропагандируются многие вещи. Например, парадокс про тело пловца. Велись обсуждения на тему того, что разные виды спорта влияют на то, как развиваются мышцы человека. Хотя на самом деле было доказано, что развитие мышц связано с генетической предрасположенностью, а, следовательно, от этого и зависел успех в том или ином виде спорта.
Возникает вопрос: еще в древние века Цицерон сказал, как рационально обдумывать данные ситуации, спустя время Даниэль Канеман (израильско-американский психолог, один из основоположников психологической экономической теории и поведенческих финансов) получил Нобелевскую премию по экономике, будучи психологом, за исследования рационального поведения. Неужели люди так и не научились поступать рационально? По данной теме много написано в книге Талеба «Черный лебедь. Под знаком непредсказуемости».
Приведем пример из древности. Когда Цицерону (древнеримскому политическому деятелю и философу) показали фреску с изображением, где люди молятся, чтобы спастись от шторма, и фреску с людьми, которые спаслись, потому что молились, он попросил изображение с людьми, которые молились и не спаслись. То есть, возвращаясь к вероятности, мы иногда видим некую часть поля событий, но из-за своих эмоциональных или психологических особенностей не видим его в целом.
С помощью этого эффекта пропагандируются многие вещи. Например, парадокс про тело пловца. Велись обсуждения на тему того, что разные виды спорта влияют на то, как развиваются мышцы человека. Хотя на самом деле было доказано, что развитие мышц связано с генетической предрасположенностью, а, следовательно, от этого и зависел успех в том или ином виде спорта.
Возникает вопрос: еще в древние века Цицерон сказал, как рационально обдумывать данные ситуации, спустя время Даниэль Канеман (израильско-американский психолог, один из основоположников психологической экономической теории и поведенческих финансов) получил Нобелевскую премию по экономике, будучи психологом, за исследования рационального поведения. Неужели люди так и не научились поступать рационально? По данной теме много написано в книге Талеба «Черный лебедь. Под знаком непредсказуемости».
Часто нерациональное поведение связано с тем, что мы не знаем или не используем простые математические закономерности. Мы можем знать о них, но не применять в реальной жизни, думая, что это совершенно другая задача. Люди зачастую неверно сводят сложившуюся ситуацию к задаче, правильное решение которой уже известно. Вот о таких ситуациях и пойдет речь.
Как глупо отыгрываться в казино (07:19)
Начнем с задачи, в которой монета подбрасывается несколько раз. Известно, что если подбрасывать монету большое количество раз, то орел и решка выпадают с одинаковой вероятностью. Представим, что мы бросали монету и 5 раз выпал орел. Что выпадет на шестой раз (Рис. 3)?

Рис. 3. Орел или решка?
Скорее всего человек с гуманитарным образованием ответит, что выпадет решка, ведь орел выпадал уже 5 раз. Это и есть ожидание выигрыша в казино (вот-вот повезет). Но на самом деле и в шестой раз вероятность выпадения орла или решки равна 1/2. Эту ситуацию можно заменить аналогичной, представив, что 6 человек подбрасывают монету. Для всех вероятность выпадения любой из сторон монеты по-прежнему 1/2, но ваш бросок не зависит от пяти предыдущих (Рис. 4).

Рис. 4. Подбрасывание монеты
Стоит заметить, вероятность того, что 5 раз выпадет решка и 1 раз орел или же 6 раз выпадет решка, разная (Рис. 5).

Рис. 5. Вероятность для двух исходов
Как мы видим, первая вероятность гораздо больше. Но тут уже вступает в силу то, что мы знаем результаты предыдущих 5 бросков. Во всех этих ситуациях мы предполагаем, что монета настоящая (нет смещения центра тяжести и т.д.).
Условная вероятность (09:41)
В предыдущих примерах мы совершали ошибку при выборе за счет того, что события казались нам зависимыми, в то время как они были независимыми. Существуют и обратные ситуации, когда нам кажется, что события независимы, но на самом деле они зависимы. Самым известным примером такой ситуации является парадокс Монти Холла. Есть 3 коробки, в одной из которых находится приз. Вы делаете выбор, после чего ведущий выбирает одну из оставшихся коробок и показывает, что она пустая. Далее вам предлагается поменять свой выбор (Рис. 6).

Рис. 6. Иллюстрация парадокса Монти Холла
Парадокс Монти Холла
Можно усилить данную формулировку, сказав, что в одной из трех коробок лежит 1000 рублей, а ведущий после сделанного выбора предлагает за 100 рублей открыть одну из пустых коробок. Стоит ли принимать такое предложение?
Кажется, что принимать такое предложение не стоит, поскольку вероятность нахождения денег в коробке от этого не поменяется, по-прежнему останется 1/3. Но на самом деле стоит согласиться. Докажем это.
Если предложить человеку, который не согласился покупать такую возможность, выбрать между одной коробкой (которую он изначально выбрал) и двумя оставшимися, то он выберет 2 (с двумя коробками вероятность выигрыша больше). В какой-то из этих двух коробок пусто, ее ведущий и откроет (Рис. 1).
Конечно, нужно помнить, что при таком исходе можно проиграть (если обе выбранные коробки пустые), но если играть много раз, то в большинстве случаев вы будете выигрывать (Рис. 2).
Дома можно воспроизвести подобную ситуацию, взяв 2 красных карты и 1 черную. Предложить родителям угадывать, где находится черная карта.
Главным моментом в данной ситуации является то, что ведущий обладает знаниями: он точно знает, где находится приз, и открывает пустую коробку (Рис. 3).
Допустим, вы выбираете первую коробку, тогда возможно всего три исхода:
Важно объяснить, почему мы не всегда выигрываем. Дело в том, что мы не предсказываем исход событий, а рассматриваем вероятность выигрыша. Это разные вещи. Если много раз сыграть, то расчет вероятности даст нам положительный результат (увеличение вероятности в два раза быстро сказывается на результате), но если сыграть один раз, то возможно проиграть.
Мы считаем, что в данной ситуации события независимы, но на самом деле, когда ведущий знает, в какой коробке приз, и открывает пустую, события становятся зависимыми.
Кажется, что принимать такое предложение не стоит, поскольку вероятность нахождения денег в коробке от этого не поменяется, по-прежнему останется 1/3. Но на самом деле стоит согласиться. Докажем это.
Если предложить человеку, который не согласился покупать такую возможность, выбрать между одной коробкой (которую он изначально выбрал) и двумя оставшимися, то он выберет 2 (с двумя коробками вероятность выигрыша больше). В какой-то из этих двух коробок пусто, ее ведущий и откроет (Рис. 1).
Конечно, нужно помнить, что при таком исходе можно проиграть (если обе выбранные коробки пустые), но если играть много раз, то в большинстве случаев вы будете выигрывать (Рис. 2).
Дома можно воспроизвести подобную ситуацию, взяв 2 красных карты и 1 черную. Предложить родителям угадывать, где находится черная карта.
Главным моментом в данной ситуации является то, что ведущий обладает знаниями: он точно знает, где находится приз, и открывает пустую коробку (Рис. 3).
Допустим, вы выбираете первую коробку, тогда возможно всего три исхода:
- приз находится во второй коробке, ведущий открывает третью,
- приз находится в третей коробке, ведущий открывает вторую,
- приз находится в первой коробке, ведущий открывает любую из оставшихся.
Важно объяснить, почему мы не всегда выигрываем. Дело в том, что мы не предсказываем исход событий, а рассматриваем вероятность выигрыша. Это разные вещи. Если много раз сыграть, то расчет вероятности даст нам положительный результат (увеличение вероятности в два раза быстро сказывается на результате), но если сыграть один раз, то возможно проиграть.
Мы считаем, что в данной ситуации события независимы, но на самом деле, когда ведущий знает, в какой коробке приз, и открывает пустую, события становятся зависимыми.

Рис. 1. Открытие пустой коробки
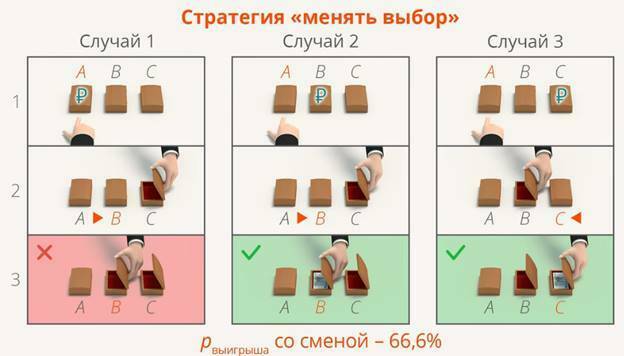
Рис. 2. Вероятность всех исходов при смене выбора

Рис. 3. Открытие пустой коробки
В обоих предыдущих примерах у нас была некоторая зависимость (или, наоборот, независимость) одних событий от других. В таком случае мы можем говорить про условную вероятность (вероятность наступления одного события при условии, что другое событие уже произошло).
Задача про щенка (10:39)
Приведем пример связанный с жизненными решениями и страхами. Допустим, по результатам анализов вашего щенка, вам сообщили, что он болен. Точность анализа Pошибки анализа = 0,001, то есть прибор ошибается в 1 случае из 1000. Какова вероятность, что ваш щенок действительно болен? Кажется, вся исходная информация дана, но на самом деле нужно еще учитывать, насколько редкое данное заболевание. Если прибор в принципе может ошибаться, значит, эта ошибка может сыграть и в нашу пользу.
Допустим из 1 000 000 собак данной болезнью болеет всего 100 собак (Pболезни = 1/1000000 = 0,0001). С другой стороны, если прибор проверит 1000000 собак, то он ошибется на 1000 из них (Pошибки анализа = 1000000 ∙ 0,001 = 1000). То есть из этой 1000 собак, для которых прибор показал наличие болезни, по-настоящему больным окажутся только 100 из них.
Pправильности анализов ⩽ 100/1000 ⩽ 10%
Получается, что правильность прибора составляет не более 10%, а значит, вероятность того, что щенок здоров после сдачи одного анализа, велика (более 90%).
Для бытового применения такой метод подходит. Если вероятность правильной работы прибора меньше 10%, то можно сдать анализы в другой клинике (на другом приборе), чтобы обеспечить независимость этих событий. Конечно, абсолютной независимости результатов сложно достигнуть, поскольку в подобных приборах зачатую используются похожие методы исследования. Но в нашей ситуации этого будет достаточно, и, если на второй раз анализы показали, что щенок болен, скорее всего, так и есть.
Допустим из 1 000 000 собак данной болезнью болеет всего 100 собак (Pболезни = 1/1000000 = 0,0001). С другой стороны, если прибор проверит 1000000 собак, то он ошибется на 1000 из них (Pошибки анализа = 1000000 ∙ 0,001 = 1000). То есть из этой 1000 собак, для которых прибор показал наличие болезни, по-настоящему больным окажутся только 100 из них.
Pправильности анализов ⩽ 100/1000 ⩽ 10%
Получается, что правильность прибора составляет не более 10%, а значит, вероятность того, что щенок здоров после сдачи одного анализа, велика (более 90%).
Для бытового применения такой метод подходит. Если вероятность правильной работы прибора меньше 10%, то можно сдать анализы в другой клинике (на другом приборе), чтобы обеспечить независимость этих событий. Конечно, абсолютной независимости результатов сложно достигнуть, поскольку в подобных приборах зачатую используются похожие методы исследования. Но в нашей ситуации этого будет достаточно, и, если на второй раз анализы показали, что щенок болен, скорее всего, так и есть.
Точная вероятность. Теорема Байеса (12:56)
Бывают ситуации, в которых нужно точно посчитать вероятность. Например, если это какая-то важная статистическая оценка или же погрешность прибора. В таких случаях используют формулу Байеса: P(A|B) = P(B|A) ∙ P(A) / P(B). Ее также называют теоремой Байеса об условной вероятности.
Воспользуемся этой формулой на примере предыдущей задачи про щенка. Нас интересует вероятность ошибки прибора, то есть ситуация, когда прибор покажет, что щенок болен, хотя на самом деле он здоров. Всего может быть 4 варианта исхода (собака может быть больна или здорова, прибор может показывать «болен» или «здоров»), они представлены в таблице 1.
Мы знаем, что одновременное происхождение двух событий – это произведение вероятностей. То есть, чтобы посчитать вероятность того, что собака больна и прибор показал «болен», нужно найти произведение этих двух вероятностей. В данном случае она ⩽ 18,2%. Зная эту вероятность, можно посчитать все остальные.
Воспользуемся этой формулой на примере предыдущей задачи про щенка. Нас интересует вероятность ошибки прибора, то есть ситуация, когда прибор покажет, что щенок болен, хотя на самом деле он здоров. Всего может быть 4 варианта исхода (собака может быть больна или здорова, прибор может показывать «болен» или «здоров»), они представлены в таблице 1.
Мы знаем, что одновременное происхождение двух событий – это произведение вероятностей. То есть, чтобы посчитать вероятность того, что собака больна и прибор показал «болен», нужно найти произведение этих двух вероятностей. В данном случае она ⩽ 18,2%. Зная эту вероятность, можно посчитать все остальные.

Таблица 1. Вероятность для всех исходов в задаче про щенка
В общем виде формула Байеса используется для двух событий. Но бывают такие задачи, в которых для одного события возможно несколько исходов. Для таких ситуаций есть обобщенная формула Байеса:

Мы рассмотрели самое наглядное применение данной формулы. Подробнее о данной формуле и случаях ее применения можно посмотреть по ссылке.
Исходя из рассмотренной задачи, становится понятно, почему в случае хороших результатов можно не делать повторный анализ. Ведь вероятность того, что прибор покажет «здоров» в случае, когда щенок действительно болен, близка к нулю.
Как мы уже выяснили, в ситуациях, когда погрешность прибора сравнима (или даже выше) с редкостью заболевания, рекомендуется выполнить повторный анализ, если первый анализ показал «болен».
Исходя из рассмотренной задачи, становится понятно, почему в случае хороших результатов можно не делать повторный анализ. Ведь вероятность того, что прибор покажет «здоров» в случае, когда щенок действительно болен, близка к нулю.
Как мы уже выяснили, в ситуациях, когда погрешность прибора сравнима (или даже выше) с редкостью заболевания, рекомендуется выполнить повторный анализ, если первый анализ показал «болен».
Где покупать молоко? (15:36)
Стоит рассмотреть еще один вопрос. Почему безопаснее покупать продукт, произведенный на большем заводе, чем на маленьком? Все дело в том, что для большого завода поле событий больше (Рис. 7) (большее количество выпускаемого товара), и если возникнут какие-либо проблемы, то на большом заводе они будут быстрее обнаружены, чем на маленьком заводе.
Следовательно, вероятность устранения ошибки до ее негативных последствий на большом заводе выше, чем эта же вероятность для маленького завода.

Рис. 7. Поле событий для большого и маленького молокозавода
Рациональность поступков и математика (17:09)
Исходя из того, что рациональность поведения тесно связана с математикой, можно сделать вывод, что все математики должны быть успешными. Но, как показывает практика, это не так. Во-первых, данные математические формулы нужно уметь интерпретировать в реальных жизненных ситуациях. Во-вторых, стоит различать понятия вероятность и предсказание. Ведь можно правильно посчитать вероятность, но это не будет предсказанием. В-третьих, недостаточно одного умения рассчитывать вероятность, нужно еще иметь решительность действовать. Кроме того, среди всех людей нематематиков больше, чем математиков, поэтому среди выигравших в какой-либо ситуации математиков все-таки меньше, чем нематематиков. Хотя известны примеры, когда математики начинали заниматься бизнесом и достигали хороших результатов.
Стоит упомянуть ситуацию, когда в лотерее выигрывал один и тот же человек дважды. С точки зрения теории вероятности шанс выиграть в лотерее стремится к 0, а вероятность повторого выигрыша близка к 0². Но жизненный опыт показывает, что даже такие маловероятные события возможны.
Стоит упомянуть ситуацию, когда в лотерее выигрывал один и тот же человек дважды. С точки зрения теории вероятности шанс выиграть в лотерее стремится к 0, а вероятность повторого выигрыша близка к 0². Но жизненный опыт показывает, что даже такие маловероятные события возможны.
Выводы (18:39)
Можем сделать очевидный вывод: прежде чем принимать какое-либо решение, стоит хорошо обдумать всю сложившуюся ситуацию. В ряде случаев вам поможет знание теоремы Байеса или же понимание подхода, который в ней используется.
Другие материалы

